Équations et inéquations du premier degré ?

Mariam Ait Merri

• juin 3, 2024

Les équations et inéquations du premier degré sont des concepts fondamentaux en mathématiques, souvent rencontrés dès les premiers cours d’algèbre au collège et tout au long de l’enseignement secondaire. Maîtriser la résolution de ces équations et inéquations est crucial, non seulement pour réussir dans les cours de mathématiques, mais aussi pour développer des compétences analytiques et de résolution de problèmes applicables dans de nombreuses disciplines et situations de la vie quotidienne. Cet article de blog vous guidera à travers les étapes clés pour résoudre efficacement les équations et inéquations du premier degré, en vous offrant des méthodes claires et des exemples pratiques pour renforcer votre compréhension et votre confiance en ces concepts essentiels. Que vous soyez un étudiant cherchant à améliorer ses compétences ou simplement quelqu’un désireux de rafraîchir ses connaissances, ce guide vous fournira les outils nécessaires pour maîtriser les bases de l’algèbre.

Résoudre les Équations du Premier Degré

A. Définition et Concepts de Base

1. Qu’est-ce qu’une équation du premier degré ?
   Une équation du premier degré, aussi appelée équation linéaire, est une équation algébrique dans laquelle la variable apparaît uniquement avec un exposant de 1. La forme générale d’une équation du premier degré est ( ax + b = 0 ), où ( a ) et ( b ) sont des coefficients constants, ( x ) est la variable, et a est différent de 0 .
2. Variables et coefficients

• Variable : L’inconnue que l’on cherche à déterminer, généralement représentée par ( x ).
• Coefficients : Les nombres ( a ) et ( b ) dans l’équation ( ax + b = 0 ). Le coefficient ( a ) est associé à la variable ( x ) et ( b ) est le terme constant.

1. L’égalité et ses propriétés

• Transposition : On peut ajouter, soustraire, multiplier ou diviser les deux côtés d’une équation par le même nombre sans changer l’égalité.
• et Symétrie : Si ( a = b ), alors ( b = a ).
• et Transitivité : Si ( a = b ) et ( b = c ), alors ( a = c ).

B. Méthodes de Résolution

1. Isolation de la variable
   Pour résoudre une équation du premier degré, l’objectif est d’isoler la variable ( x ) d’un côté de l’équation. Voici les étapes générales :

• Déplacer tous les termes contenant ( x ) d’un côté de l’équation et les termes constants de l’autre côté.
• Simplifier l’équation pour isoler ( x ).

1. Utilisation des opérations inverses

• Addition et soustraction : Si un terme est ajouté à ( x ), soustrayez ce terme des deux côtés. Si un terme est soustrait, ajoutez-le des deux côtés.
• Multiplication et division : Si ( x ) est multiplié par un coefficient, divisez les deux côtés par ce coefficient pour isoler ( x ). Si ( x ) est divisé par un coefficient, multipliez les deux côtés par ce coefficient.

1. Exemples pratiques de résolution

Exemple 1 : Résoudre ( 2x + 5 = 15 )

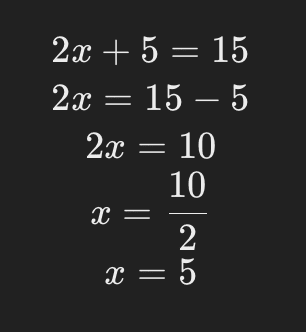
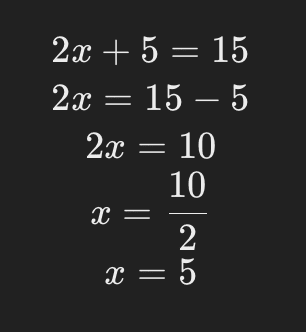
Exemple 2 : Résoudre ( -3x + 7 = 1 )

C. Applications Pratiques

Problèmes de la vie quotidienne

• Exemple : Calculer le coût total de produits avec un prix fixe plus des frais supplémentaires.

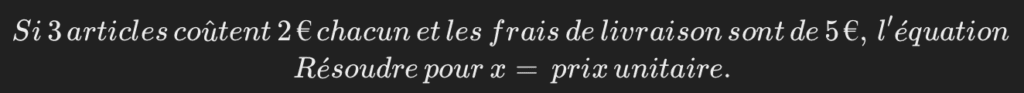
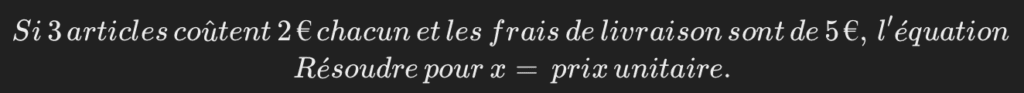
Applications en sciences et ingénierie

• Exemple : Déterminer la tension électrique nécessaire pour obtenir un courant spécifique dans un circuit électrique en utilisant la loi d’Ohm (( V = IR )).

En comprenant ces méthodes et applications, vous pouvez résoudre efficacement les équations du premier degré et appliquer ces compétences dans divers contextes pratiques.

Résoudre les Inéquations du Premier Degré

A. Définition et Concepts de Base

1. Qu’est-ce qu’une inéquation du premier degré ?
   Une inéquation du premier degré, également appelée inéquation linéaire, est une expression mathématique qui établit une relation d’ordre entre deux expressions linéaires. La forme générale d’une inéquation du premier degré est ( ax + b < c ) (ou ( \leq ), ( > ), ( \geq )), où ( a ) et ( b ) sont des coefficients constants, ( x ) est la variable, et ( c ) est un terme constant.
2. Différence entre équations et inéquations

• Équation : Égalité entre deux expressions (( ax + b = c )).
• Et Inéquation : Relation d’ordre entre deux expressions (( ax + b < c ), ( ax + b > c ), ( ax + b \leq c ), ( ax + b \geq c )).

1. Symboles d’inégalité

• ( < ) : moins que
• ( \leq ) : moins que ou égal à
• ( > ) : plus que
• ( \geq ) : plus que ou égal à

B. Méthodes de Résolution

1. Isolation de la variable
   La résolution d’une inéquation du premier degré implique d’isoler la variable ( x ) d’un côté de l’inéquation. Les étapes sont similaires à celles utilisées pour résoudre une équation, mais il faut prêter attention aux règles spécifiques des inégalités.
2. Utilisation des opérations inverses en respectant les règles d’inégalité

• Addition et soustraction : On peut ajouter ou soustraire le même nombre des deux côtés de l’inéquation sans changer le sens de l’inégalité.
• Et Multiplication et division : Lorsque l’on multiplie ou divise les deux côtés d’une inéquation par un nombre positif, le sens de l’inégalité reste inchangé. Si l’on multiplie ou divise par un nombre négatif, le sens de l’inégalité doit être inversé.

Exemples pratiques de résolution

Exemple 1 : Résoudre ( 2x + 5 < 15 )

Exemple 2 : Résoudre ( -3x + 7 \geq 1 )

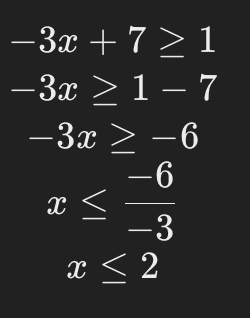
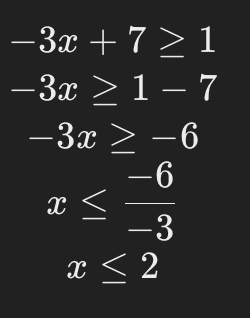
C. Représentation Graphique et Applications Pratiques

1. Représentation des solutions sur une droite numérique

• Les solutions d’une inéquation peuvent être sur une droite numérique. On utilise des parenthèses ouvertes pour ( < ) et ( > ) et des crochets fermés pour ( \leq ) et ( \geq ).
• donc Exemple : Pour ( x < 5 ), on dessine une parenthèse ouverte sur 5 et une ligne vers la gauche.
• ou Exemple : Pour ( x \leq 2 ), on dessine un crochet fermé sur 2 et une ligne vers la gauche.

1. Applications pratiques et interprétation des résultats

• Applications pratiques : Les inéquations sont utilies pour résoudre des problèmes de contraintes, comme déterminer les plages de prix acceptables. Et aussi les quantités maximales ou minimales de produits. Ou les seuils de performance.
• Exemple : Supposons que pour fabriquer un produit, les coûts doivent être inférieurs à 100 €. Si le coût de production est donné par ( 20x + 30 ), où ( x ) est le nombre d’unités produites, l’inéquation est ( 20x + 30 < 100 ). En résolvant, on trouve ( x < 3.5 ), ce qui signifie que pour maintenir les coûts en dessous de 100 €, on peut produire au maximum 3 unités.

Donc en maîtrisant la résolution des inéquations du premier degré, on peut analyser et interpréter des situations réelles de manière mathématique. Et c’est ce qui est essentiel dans de nombreux domaines pratiques et professionnels.