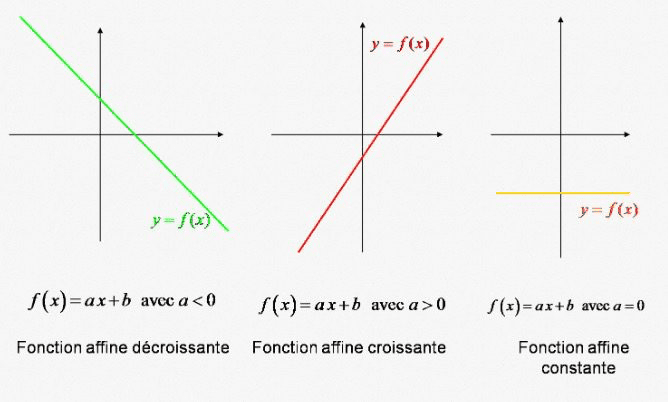

Les fonctions affines et linéaires sont des outils fondamentaux qui sous-tendent de nombreuses branches des mathématiques. Et elles trouvent des applications dans divers domaines. Leur étude permet de résoudre une multitude de problèmes. Qu’il s’agisse de modéliser des phénomènes naturels, d’analyser des données ou de comprendre des concepts théoriques. En effet, ces fonctions sont omniprésentes dans l’algèbre, la géométrie et l’analyse. Offrant ainsi une base solide pour explorer des concepts plus avancés. Leur importance ne se limite pas seulement aux mathématiques pures. Mais s’étend également à des disciplines telles que la physique, l’économie, l’ingénierie et les sciences sociales.
Comprendre les propriétés et les caractéristiques distinctes des fonctions affines et linéaires est crucial pour résoudre des problèmes variés. Les fonctions linéaires, caractérisées par leur comportement préservant l’addition et la multiplication par un scalaire. Offrent une approche élégante pour modéliser des systèmes où les changements sont proportionnels. D’autre part, les fonctions affines ajoutent une composante constante. Introduisant ainsi des notions de translation et de décalage par rapport aux fonctions linéaires. Cette flexibilité les rend particulièrement utiles pour modéliser des situations où des facteurs supplémentaires doivent être pris en compte. Comme dans les problèmes financiers ou les études statistiques.
Au-delà de leur utilité pratique, l’étude des fonctions affines et linéaires revêt également une importance théorique considérable. Ces concepts constituent souvent le point de départ pour explorer des structures mathématiques plus complexes. Comme les espaces vectoriels, les transformations linéaires ou les équations différentielles. Ainsi, en approfondissant notre compréhension de ces fonctions de base, nous enrichissons notre capacité à aborder des problèmes mathématiques et scientifiques plus avancés. Tout en développant notre intuition quant aux relations fondamentales qui sous-tendent notre univers mathématique.
Les Fonctions Linéaires
Commençons par les fonctions linéaires, qui sont parmi les plus simples et les plus importantes en mathématiques. Une fonction linéaire est une fonction qui satisfait deux propriétés fondamentales : l’additivité et l’homogénéité.
Soit f une fonction définie sur un espace vectoriel V sur un corps K. f est dite linéaire si pour tout x et y dans V et tout scalaire k dans K, les deux propriétés suivantes sont vérifiées :
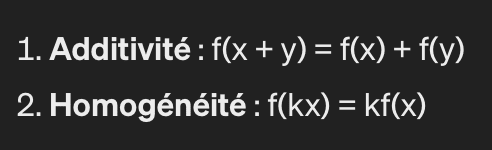
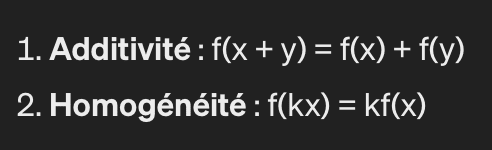
En d’autres termes, une fonction est linéaire si elle préserve l’addition et la multiplication par un scalaire. L’exemple le plus simple de fonction linéaire est la fonction identité, où f(x) = x.
Les fonctions linéaires sont omniprésentes dans de nombreux domaines des mathématiques et des sciences. Elles sont utilisées pour modéliser des phénomènes physiques, économiques et sociaux. Par exemple, dans le domaine de l’algèbre linéaire, les transformations linéaires sont étudiées en profondeur pour comprendre les propriétés des matrices et des espaces vectoriels.
Les Fonctions Affines
Les fonctions affines sont une généralisation des fonctions linéaires qui inclut une composante constante. Donc une fonction f est dite affine si elle peut être écrite sous la forme :
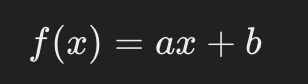
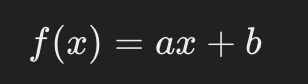
Où a et b sont des constantes réelles, avec a ≠ 0. Et la présence de la composante b distingue les fonctions affines des fonctions linéaires. Car cette composante constante donne à la fonction affine une sorte de “décalage” par rapport à une fonction linéaire.
Et aussi une propriété importante des fonctions affines est qu’elles préservent les rapports de distances. Donc cela signifie que si vous avez deux points sur une droite, les rapports des distances entre ces points seront les mêmes sur la droite d’arrivée après l’application d’une fonction affine.
Les fonctions affines sont largement utilisées dans de nombreux domaines, y compris les sciences économiques, l’ingénierie, la physique et la statistique. Par exemple, dans le domaine de la finance, les fonctions affines sont utilisées pour modéliser les taux d’intérêt et les processus stochastiques.
Conclusion
En résumé, les fonctions affines et linéaires constituent des piliers fondamentaux des mathématiques. Elles sont indispensables dans de nombreux domaines d’application. Leur compréhension profonde est essentielle pour aborder une multitude de problèmes mathématiques et pour élaborer des modèles précis dans des contextes réels. De l’algèbre à la géométrie en passant par l’analyse, ces fonctions jouent un rôle crucial dans la résolution de problèmes variés.
Chez SmartProf, notre équipe de professeurs de mathématiques qualifiés est prête à vous guider dans votre compréhension des fonctions affines et linéaires. Donc ainsi que dans de nombreux autres domaines des mathématiques. Avec une approche pédagogique personnalisée et interactive, nos experts sont là pour répondre à toutes vos questions et vous aider à progresser dans votre parcours mathématique. Explorez notre plateforme dès aujourd’hui pour accéder à des ressources d’apprentissage de qualité et à un soutien individualisé pour exceller dans les mathématiques et au-delà.



