Fonction Exponentielle : Fondements et Applications

Mariam Ait Merri

• avril 22, 2024

La fonction exponentielle transcende les frontières disciplinaires, s’imposant comme l’un des piliers incontournables des mathématiques appliquées. Sa portée va bien au-delà des théories abstraites. Elle infuse chaque domaine du savoir, des sciences pures à l’ingénierie, de l’économie à la biologie. Son omniprésence témoigne de sa capacité unique à saisir et à modéliser des phénomènes d’une diversité étonnante, de la croissance cellulaire à l’évolution des marchés financiers. La simplicité élégante de sa définition cache une profondeur conceptuelle. Et elle offre une perspective unifiée sur des problèmes aussi divers que la croissance exponentielle, la décomposition radioactive ou même la diffusion de l’information dans les réseaux sociaux. En tant que tel, l’étude de la fonction exponentielle dépasse largement le cadre des équations et des calculs. Car elle incarne une exploration continue des mécanismes sous-jacents à la dynamique du monde qui nous entoure. Donc illuminant les voies de la connaissance et de la découverte.

Fondements de la Fonction Exponentielle

La fonction exponentielle est ancrée dans des fondements mathématiques profonds qui la rendent incontournable dans de nombreuses applications. Son essence repose sur une série d’axiomes et de définitions qui lui confèrent des propriétés remarquables.

Tout d’abord, la fonction exponentielle est définie comme la somme infinie des termes de la série exponentielle :

Cette définition, initialement introduite par Leonard Euler au XVIIIe siècle, est cruciale car elle établit un lien profond entre l’exponentielle et le concept de limite, démontrant ainsi son caractère intrinsèquement lié à la croissance continue.

La base de l’exponentielle, qu’on note (e), est une constante mathématique fondamentale. On la connait également sous le nom de nombre d’Euler ou nombre de Néper. Sa valeur est approximativement égale à (2.71828). Et on la définie comme la limite de la fonction exponentielle lorsque l’exposant approche l’infini :

Cette définition élève (e) au rang de constantes transcendantes. Donc rejoignant les rangs prestigieux de π et (i) dans le panthéon mathématique.

En outre, la fonction exponentielle possède des propriétés remarquables qui en font un outil précieux dans l’analyse mathématique. Par exemple, elle présente une croissance exponentielle. Ce qui signifie que (e^x) augmente de manière exponentielle lorsque x augmente.

De plus, sa dérivée est égale à elle-même, c’est-à-dire que :

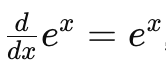
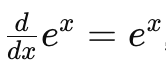
Ce qui la rend extrêmement utile dans la résolution d’équations différentielles et dans la modélisation de phénomènes dynamiques.

En comprenant ces fondements, on peut saisir la puissance et l’universalité de la fonction exponentielle. Car elle transcende les frontières disciplinaires pour devenir un pilier inébranlable de la pensée mathématique moderne.

Pour mieux comprendre ces propos, vous pouvez faire appel à l’assistance des professeurs de mathématiques de Smartprof pour une réussite académique assurée.

Propriétés et Caractéristiques

Cette fonction est riche en propriétés et caractéristiques qui la rendent indispensable dans de nombreux domaines mathématiques et scientifiques. Voici quelques-unes des propriétés les plus remarquables :

1. Croissance exponentielle : L’une des caractéristiques les plus fondamentales de la fonction exponentielle est sa croissance exponentielle. Cela signifie que lorsque (x) augmente, (e^x) augmente de manière exponentielle, ce qui en fait un modèle efficace pour décrire des phénomènes de croissance rapide tels que la population, les infections virales ou même la valeur des investissements financiers.
2. Dérivée constante : La dérivée de la fonction exponentielle est égale à elle-même. Formellement, (\frac{d}{dx} e^x = e^x). Cette propriété est extrêmement utile dans la résolution d’équations différentielles et dans l’analyse de systèmes dynamiques, où la fonction exponentielle émerge fréquemment comme une solution naturelle.
3. Relation avec les logarithmes : La fonction exponentielle et les logarithmes sont étroitement liés en tant qu’opérations inverses l’une de l’autre. Cela signifie que si (y = e^x), alors (x = \log(y)) où (\log) représente le logarithme naturel. Cette relation est cruciale dans de nombreux contextes, notamment en résolvant des équations exponentielles ou en transformant des équations complexes en formes plus gérables.
4. Propriété d’identité : Pour tout réel (x), (e^0 = 1). Cela signifie que l’exponentielle de zéro est égale à un, une propriété qui joue un rôle crucial dans de nombreuses preuves et démonstrations mathématiques.
5. Propriété d’inversibilité : La fonction exponentielle est une fonction injective, ce qui signifie qu’elle est inversible sur son domaine. En d’autres termes, chaque valeur de (x) correspond à une et une seule valeur de (e^x), ce qui garantit que la fonction exponentielle peut être inversée pour obtenir la valeur originale de (x).

Ces propriétés et caractéristiques témoignent de la polyvalence et de la puissance de la fonction exponentielle, en faisant un outil indispensable dans de nombreux domaines des mathématiques et des sciences.

Applications de la Fonction Exponentielle dans la Vie Courante

La fonction exponentielle trouve des applications répandues et cruciales dans de nombreux aspects de la vie quotidienne. Car de la finance à la biologie en passant par l’ingénierie, elle se prouve utile. Une application majeure réside dans la modélisation de la croissance exponentielle de la population. Car en utilisant des modèles basés sur la fonction exponentielle, les démographes peuvent estimer la croissance future de la population mondiale. Ainsi que les tendances démographiques dans des régions spécifiques. Donc ce qui aide à orienter les politiques publiques en matière de santé. Et aussi d’éducation et de développement économique.

Dans le domaine financier, la fonction exponentielle est omniprésente dans la modélisation des intérêts composés. Les intérêts composés, où les intérêts sont calculés non seulement sur le montant initial investi. Mais aussi sur les intérêts accumulés précédemment, suivent un schéma de croissance exponentielle. Cette caractéristique est largement utilisée dans le calcul de la valeur future des investissements. Et aussi des prêts, des hypothèques et des pensions. Donc permettant aux individus et aux institutions financières de planifier leurs investissements à long terme de manière efficace.

En outre, la fonction exponentielle est utilisée dans des domaines tels que la cinétique chimique pour modéliser la vitesse des réactions chimiques. Ou dans l’ingénierie pour décrire la décroissance radioactive des matériaux. Et même dans l’analyse des réseaux sociaux pour représenter la diffusion virale de l’information. Son rôle essentiel dans ces divers domaines souligne son importance universelle. Et aussi sa pertinence dans la compréhension et la modélisation de phénomènes dynamiques dans le monde réel.

Conclusion

En conclusion, la fonction exponentielle émerge comme un pilier fondamental de la pensée mathématique et de la modélisation scientifique. De ses fondements élégants à ses applications diverses et omniprésentes dans la vie quotidienne, elle incarne la puissance et l’universalité des principes mathématiques. Sa capacité à capturer des phénomènes de croissance rapide, sa relation étroite avec les logarithmes et sa constante présence dans des domaines aussi variés que la finance, la démographie et la cinétique chimique témoignent de son importance vitale.

L’étude et la compréhension de la fonction exponentielle transcendent les limites de la simple théorie mathématique. Elles nous invitent à explorer les mécanismes profonds qui régissent le monde qui nous entoure, des populations en croissance exponentielle aux marchés financiers en évolution constante. En tant qu’outil essentiel, la fonction exponentielle éclaire notre compréhension du présent et nous aide à anticiper et à façonner l’avenir. Ainsi, que ce soit dans les laboratoires de recherche, les salles de classe ou les bureaux de planification, la fonction exponentielle demeure une alliée indispensable pour ceux qui cherchent à percer les mystères du monde quantifiable.