Le Théorème de Pythagore et sa Contraposée

Mariam Ait Merri

• février 19, 2024

Le théorème de Pythagore est un joyau des mathématiques, transmis depuis l’antiquité. Ce principe, attribué au mathématicien grec Pythagore, révèle une relation fondamentale en géométrie. Dans cet article, nous allons découvrir le théorème qui a marqué un tournant dans l’histoire des mathématiques, influençant d’innombrables domaines et restant un pilier de l’éducation mathématique moderne. Mais d’abord, disons bonjour à Mr Pythagore :

https://www.babelio.com/auteur/-Pythagore/99274

1 – Comprendre le Théorème de Pythagore.

1 – Définition du théorème

Le théorème de Pythagore est une pierre angulaire des mathématiques, célèbre pour sa simplicité et son utilité immense. En termes simples, ce théorème énonce que dans un triangle rectangle, la somme des aires des carrés construits sur les deux côtés les plus courts, appelés cathètes, est égale à l’aire du carré construit sur le côté le plus long, nommé hypoténuse. Cette relation est souvent représentée par la formule a² + b² = c², où a et b sont les longueurs des cathètes et c celle de l’hypoténuse. Cette formule fondamentale est non seulement un outil crucial en géométrie et en trigonométrie, mais elle sert également de passerelle vers des concepts plus avancés en mathématiques.

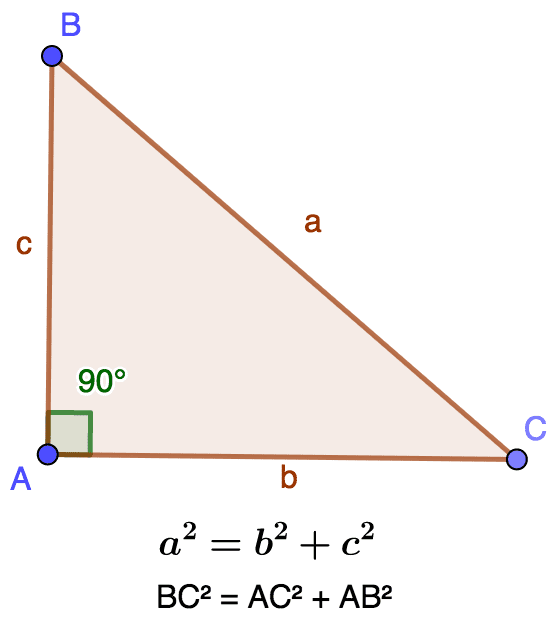
2 – Histoire du théorème

L’histoire du théorème de Pythagore remonte à bien avant Pythagore lui-même, qui a vécu autour du 6ème siècle avant J.-C. Des preuves archéologiques suggèrent que les Babyloniens et les Égyptiens connaissaient déjà les principes du théorème, plusieurs siècles avant Pythagore. Cependant, c’est Pythagore, ou peut-être ses disciples, qui est crédité de la première preuve formelle de ce théorème. Cette découverte a été une véritable révolution dans le monde des mathématiques de l’époque, marquant un pas significatif de l’abstraction mathématique vers la démonstration rigoureuse.

Ce théorème a joué un rôle crucial dans le développement des mathématiques. Il a ouvert la voie à l’exploration de concepts plus complexes et a posé les fondations pour la géométrie euclidienne. Plus qu’une simple relation entre les côtés d’un triangle, il incarne l’émergence de la pensée logique et déductive en mathématiques. Son universalité et sa capacité à relier la géométrie à l’algèbre en font un des théorèmes les plus puissants et les plus influents de l’histoire des mathématiques.

Au fil des siècles, le théorème de Pythagore a non seulement survécu, mais il a aussi évolué, influençant de nombreux domaines allant de la construction architecturale à la navigation, et continuant à être un sujet d’enseignement et d’étude essentiel dans l’éducation moderne en mathématiques.

2 – Applications Réelles du Théorème de Pythagore

Le théorème de Pythagore, une pierre angulaire des mathématiques, se révèle être un outil inestimable dans une multitude de scénarios pratiques, bien au-delà des salles de classe et des manuels théoriques. Son application quotidienne s’étend de la construction et l’architecture à des domaines aussi divers que la navigation, l’urbanisme et même les sports.

En architecture et construction, ce théorème est essentiel pour garantir que les angles des structures sont droits. Les architectes et les ingénieurs l’utilisent pour calculer des distances précises et pour s’assurer que les éléments comme les murs, les sols et les toits sont parfaitement alignés et équilibrés. Dans la navigation, le théorème aide à déterminer la distance la plus directe entre deux points, permettant ainsi aux navires et aux avions de tracer des routes plus efficaces et économiques.

En urbanisme, le théorème de Pythagore est un allié précieux pour la conception de plans de villes, l’optimisation des réseaux de routes et la planification d’espaces comme les parcs et les espaces de loisirs, où la disposition des chemins et des installations doit être à la fois esthétique et fonctionnelle. De même, dans le domaine de la topographie, il aide à mesurer des terrains et à cartographier des zones géographiques avec précision.

Au delà des applications professionnelles de Pythagore

Au-delà de ces applications professionnelles, le théorème trouve son utilité dans la vie de tous les jours. Par exemple, lors de l’installation d’une étagère ou de l’aménagement d’un jardin, l’application de ce principe permet de s’assurer que les éléments sont droits et harmonieux. Dans les sports, comme le billard ou le golf, comprendre et appliquer les principes du théorème peut améliorer la précision et la stratégie du jeu. Les photographes l’utilisent aussi pour calculer des angles et des perspectives, assurant ainsi une composition équilibrée de leurs images.

Même dans le monde de la technologie, le théorème de Pythagore joue un rôle important. Dans le développement de jeux vidéo et la création d’effets spéciaux, il est utilisé pour calculer des trajectoires, des ombres et des perspectives, contribuant à rendre ces mondes virtuels plus réalistes et immersifs.

En résumé, le théorème de Pythagore, bien que concept mathématique ancien, continue de se manifester dans de nombreux aspects de notre vie moderne. Son ubiquité et sa polyvalence témoignent de la beauté et de la puissance des mathématiques, un langage universel qui relie des domaines apparemment disparates de notre quotidien.

3 – Découverte de la Contraposée du Théorème de Pythagore

La contraposée est une proposition logique qui résulte de la négation simultanée des termes de la conclusion et de l’hypothèse d’une déclaration donnée. Formellement, si l’on a une affirmation du type “Si P alors Q”, alors sa contraposée est “Si non-Q alors non-P”. Cela signifie que si la conclusion n’est pas vraie, alors l’hypothèse correspondante ne peut pas être vraie non plus. La contraposée permet de déduire des informations supplémentaires à partir d’une déclaration originale, en élargissant la portée de la logique conditionnelle.

En géométrie, la contraposée joue un rôle crucial dans la vérification des propriétés des triangles. Par exemple, considérons la proposition “Si un triangle est équilatéral, alors tous ses côtés sont égaux”. La contraposée de cette déclaration serait “Si un triangle n’a pas tous ses côtés égaux, alors il n’est pas équilatéral”. Ainsi, en utilisant la contraposée, on peut confirmer la validité d’une propriété en vérifiant la négation de ses éléments constitutifs. Cela simplifie la démonstration et la compréhension des relations géométriques, offrant une méthode logique et systématique pour explorer les caractéristiques des formes géométriques.

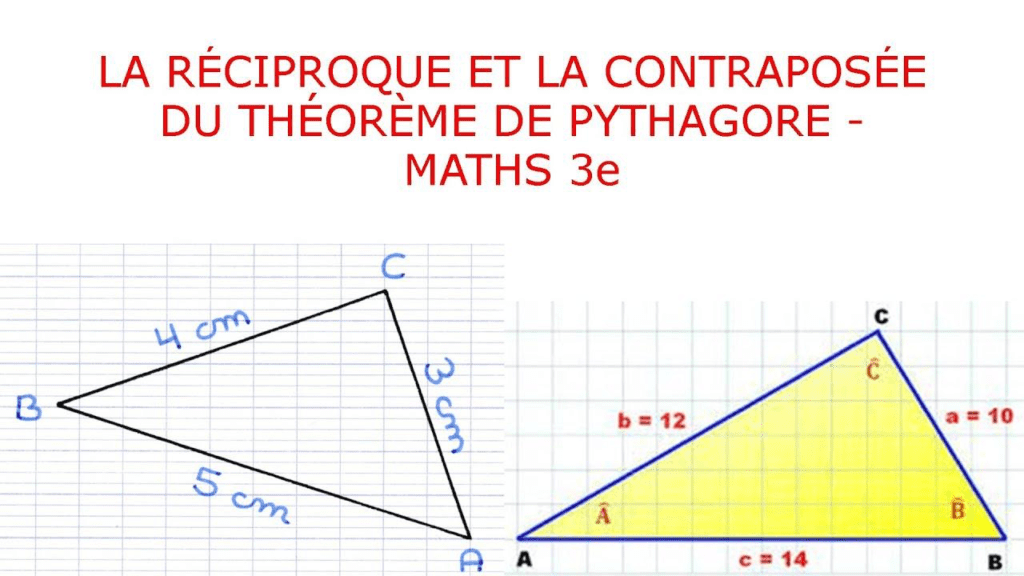
4 – Le Théorème de Pythagore dans l’Éducation Moderne

Le Théorème de Pythagore demeure un élément incontournable des programmes scolaires de mathématiques, occupant une position cruciale dans l’enseignement moderne. Sa pertinence transcende la simple géométrie, jouant un rôle essentiel dans le développement des compétences mathématiques fondamentales des étudiants. En tant que pilier de la géométrie, le théorème établit une connexion tangible entre les longueurs des côtés d’un triangle rectangle, introduisant les étudiants aux concepts géométriques fondamentaux.

Au-delà de la géométrie, le Théorème de Pythagore offre des applications pratiques significatives. Il est souvent utilisé dans la résolution de problèmes du monde réel, permettant aux étudiants de calculer des distances, de mesurer des angles, et de résoudre diverses situations liées à la distance dans l’espace tridimensionnel. En abordant ces applications concrètes, les étudiants découvrent la puissance du théorème dans la modélisation mathématique de situations de la vie quotidienne.

De plus, l’étude du Théorème de Pythagore sert de point d’entrée à la preuve mathématique. En démontrant le théorème, les étudiants développent des compétences essentielles en matière de raisonnement logique, un aspect fondamental de la pensée mathématique. Cette introduction à la preuve mathématique pave la voie pour des études plus avancées, renforçant la compréhension globale des étudiants envers la rigueur et la logique mathématique.

En somme, le Théorème de Pythagore, avec son rôle clé dans la géométrie, ses applications pratiques, et son importance dans le développement des compétences en preuve, demeure une pierre angulaire dans l’éducation mathématique moderne, préparant les étudiants à une exploration approfondie des concepts mathématiques avancés.

Conclusion

Le Théorème de Pythagore, attribué à Pythagore mais enraciné dans des connaissances plus anciennes, demeure un pilier de l’éducation mathématique. Cette simple relation a² + b² = c², démontrant l’équivalence des aires dans un triangle rectangle, transcende son rôle géométrique.
Et au-delà des salles de classe, il trouve des applications essentielles dans des domaines aussi variés que l’architecture, la navigation, l’urbanisme, les sports, et même la technologie. Donc le Théorème de Pythagore continue de jouer un rôle clé dans l’éducation moderne. Il offre une introduction à la preuve mathématique, et explore des perspectives alternatives avec sa contraposée. Mais demeure aussi un guide précieux pour comprendre les relations dans le monde mathématique. Son ubiquité et sa polyvalence attestent de son statut intemporel dans le panorama mathématique mondial.

Si vous êtes des amateurs des mathématiques ou si vous avez besoin d’assistance pour vos cours de maths, vous pouvez consulter la plateforme SmartProf et bénéficier des services de nos professeurs distingués.